Há sete enigmas da Matemática que ninguém consegue decifrar. Ninguém; ponto e vírgula! A conjetura de Poincaré é, até agora, o único que foi resolvido pelo russo Grigori Perelman. Vale a pena, por isso, conhecer este génio da matemática. Mas cuidado com as expetativas. Despenteado, rezingão e maltrapilho, ele recusou prémios milionários, cargos, honras e sumiu do mapa. Para perceber a razão do seu mau feitio é só seguir o rasto dele até São Petersburgo, na Rússia.
Encafuado em casa, Grigori Perelman está tão concentrado a testar as teorias dele, que até se esquece de tomar banho, cortar a barba, as unhas e o cabelo. Pior ainda, passa dias a fio sem comer uma única refeição de jeito. Muitas vezes, quando o estômago ronca, despacha uma sandes de queijo, bebe um copo de leite e já está. Nem fruta, nem sopa, nada.
A criatura só tem cabeça para uma única pergunta: qual é a solução para o enigma que Jules Henri Poincaré [1] lançou há 100 anos? O matemático francês que anda a tirar o sono ao matemático russo estimou, em 1902, que qualquer superfície sem furos e com três dimensões pode ser transformada numa esfera. Os cientistas que vieram depois concordam com ele, mas ainda ninguém conseguiu demonstrar que estava certo.
Na Matemática, as coisas funcionam mesmo assim: pode-se ter muita certeza do que se está a dizer, mas se não se conseguir provar, nada feito. O máximo que pode acontecer é classificarem a teoria de «conjetura», se ela for demonstrável pela lógica, e usar outros «teoremas» para, por fim, prová-la como verdadeira.
Grigori Perelman acredita que pode vir fazer isso, tal como muito outros matamáticos a trabalhar em várias partes do mundo. Ele não é o único nem tão pouco o primeiro a tentar. Muitos passam também noites e dias a rabiscar fórmulas, cálculos e equações sem chegarem a lado nenhum. O desafio é tão complicado que a Conjetura de Poincaré [2] é um dos sete problemas matemáticos mais difíceis de sempre [3]. Até há uma fundação privada em Cambridge, o Instituto de Matemática Clay, disposta a oferecer um prémio de 1 milhão de dólares ao génio que conseguir resolver algum deles.
Grigori Perelman leva sete anos a desvendar o mistério, mas, em vez de publicar o resultado numa revista científica, como fazem os ilustres cientistas, despeja todo o trabalho num site criado especialmente para os especialistas da matéria avaliarem o trabalho de outros colegas. Nas grandes universidades da Europa, da Ásia e dos Estados Unidos, uma parte dos investigadores acha estranho e comenta o caso nos corredores:
– O Perelman devia ter seguido os procedimentos normais –, criticam os académicos –, afinal, ele já é um cromo da Matemática [4] e aquele site é apenas para os que estão em início de carreira. Grigori está-se nas tintas para esse tipo de cerimónias. O que ele quer é que qualquer colega, novato ou experiente, examine o trabalho e tente encontrar erros, falhas ou esquecimentos. E, se nada encontrarem, então que deixem as formalidades de lado e anunciem o fim do mistério.
Foram precisos quatro anos para chegar o primeiro reconhecimento.
Em 2006, é-lhe atribuída Medalha Fields, considerado o Nobel da Matemática. Só que ele recusa. Sem qualquer explicação. É o primeiro a rejeitar o prémio desde que a distinção foi criada em 1935. Toda a gente fica boquiaberta, mas mais pasmada fica quando, quatro anos mais tarde, Grigori, com 43 anos, não aceita também o prémio de 1 milhão de dólares do Instituto de Matemática Clay.
Querem todos saber o que se passa com o homem. Para quê tanto esforço em descodificar um dos maiores desafios da matemática moderna e depois não ligar nenhuma à proeza? Jornalistas das televisões, dos jornais e das rádios fazem esperas à porta da casa dele, tentam contactá-lo por telefone, por email e nem um pio dele se ouve. Grigori Perelman não sai do apartamento, a não ser em escapadelas solitárias para apanhar cogumelos nos bosques, um velho hábito que nunca largou. Se calhar, são esquisitices de génios, de tão brilhantes que são, acabam cheios de manias.
A armadura do matemático
O matemático russo pouco ou nada liga aos comentários. Eles que falem até a poeira assentar. Parece que Grigori Perelman não precisa de ninguém. Se calhar, julga-se melhor do que os outros. Engano puro. Debaixo da carapaça de rezingão, está um homem desencantado, um cientista que gostaria que as pessoas ligassem mais ao trabalho dele do que ao seu feitio de bicho-do-mato.
Um dia, um jornalista de um diário russo faz um choradinho à mãe dele e consegue uma entrevista em exclusivo. Grigori Perelman não desmonta logo a armadura. Ainda refila contra tudo e todos nos primeiros minutos da conversa. Arma-se ao pingarelho. «Se sei como controlar o Universo, porque hei-de correr atrás de um milhão, diga-me?», responde quando lhe perguntam a razão para recusar o prémio atribuído em março de 2010. Mas, aos poucos, vai mostrando como está desiludido com as pessoas em geral e com os jornalistas em particular.
Toda a gente só quer saber por que não quis o dinheiro, por que não corta o cabelo, por que tem o casaco coçado ou a camisola com borbotos, se toma banho e outras coisas da vida privada que nada têm a ver com a ciência. E a ciência é o único motivo pelo qual está disposto a falar.
Perelman recebeu, nos anos seguintes, uma chuva de ofertas – prémios, cargos, honras, convites para conferências e promessas de fundos milionários para desenvolver novas pesquisas. Recusou tudo, retirou-se da vida pública e despareceu do mapa. Há mais de uma década que ninguém ouve falar dele.
«A fama e o dinheiro não me interessam – disse ele – só me distraem das coisas importantes.»
Importantes como o quê? – Gostávamos nós de saber. Por que anda um homem tantos anos obcecado à procura de uma resposta que nem sabemos muito bem para que serve? Explicar a utilidade desta descoberta para quem não é perito é tarefa bem complicada. Mas, para os especialistas, a demonstração da conjetura de Poincaré, além de muito concisa e elegante, facilita futuras investigações de processos físicos da natureza altamente complexos.
Não é à toa que é também conhecida como a Fórmula do Universo. Vivemos num mundo a três dimensões [5] e, como tal, a conjetura de Poincaré também dá a resposta à pergunta sobre a forma e a criação do Universo e quantas formas pode ele assumir. Haverá mistério maior e mais importante do que esse?
Notas de rodapé
[1] 
Jules Henri Poincaré era um daqueles cromos da ciência com talento para quase tudo. Além de especialista em muitas áreas da Matemática, formou-se em Engenharia e deixou contribuições em várias disciplinas como a Física, a Astronomia ou a Filosofia. No campo da mecânica fez trabalhos sobre as teorias da luz e as ondas eletromagnéticas. Poincaré viveu entre 1854 e 1912 e, com 48 anos, lançou um dos maiores enigmas da Matemática, que nem ele próprio conseguiu demonstrar. Também escreveu diversas obras de divulgação científica que foram bastante populares, como Ciência e Hipótese (1902), O valor da Ciência (1904) e Ciência e Método (1908).
[2] 
A conjetura de Poincaré tem a ver com um ramo da Matemática a que se dá o nome de topologia – estudo das características que certos objetos conservam mesmo depois de serem deformados. Por exemplo, uma bola de futebol ou uma casca de laranja, mesmo que espalmados, esticados ou retorcidos, nunca deixam de ser esferas (superfícies com todos os pontos à mesma distância do centro).
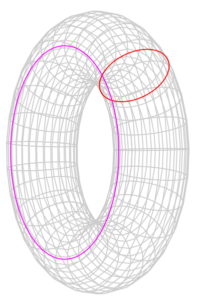
Ou seja, ambos os objetos podem retomar a forma arredondada desde que não tenham sido rasgados ou furados. No caso da bola, seria preciso enchê-la com ar para recuperar a sua forma; à laranja bastaria reconstruír a casca até à sua forma original. Nem todos os objetos têm essa característica, como aqueles com um buraco no centro – o caso de um pneu ou de uma argola de cortina. O significado do teorema demonstrado por Grigori Perelman é que, para qualquer corpo a três dimensões sem furos, há uma transformação que lhe permite sem cortes, colagens ou remendos, transformar-se numa bola.
[3] Os 7 Problemas do Milénio são: 1 – P versus NP; 2 – A conjetura de Hodge; 3 – A conjetura de Poincaré (resolvido por Grigori Perelman); 4 – A hipótese de Riemann; 5 – A existência de Yang-Mills e a falha na massa; 6 – A existência e suavidade de Navier-Stokes; 7 – A conjectura de Birch e Swinnerton-Dyer.
O Instituto Clay de Matemáticas lançou, em 2000, sete desafios, selecionados por um comité de matemáticos, anunciando prémios de um milhão de dólares para quem encontrar a resolução. Grigori Perelman resolveu um deles e Michael Atiyah anunciou, em 2018, ter encontrado a fórmula que prevê o seguinte número primo dentro de uma série de algarismos – hipótese de Riemann. O trabalho de Atiyah está ainda a ser verificado por outros colegas, mas, entretanto, o matemático britânico morreu no ano seguinte com 89 anos.
[4] 
Muito antes de encontrar a resposta para a conjetura de Poincaré, Perelman já era bastante conhecido entre os colegas. Logo após terminar os estudos, começou a trabalhar no conceituado Leningrad Department of Steklov Institute of Mathematics da Academia de Ciências da então União Soviética. Até ao início dos anos 1990 do século passado, ocupou cargos de investigação em várias universidades dos Estados Unidos. Em 1991, Grigori Perelman ganhou o Young Mathematician Prize da Sociedade Matemática de São Petersburgo. Em 1992, foi convidado para trabalhar no Instituto Courant de Ciências Matemáticas e na Universidade de Nova Iorque. Em 1995, voltou para o Instituto de Steklov, em São Petersburgo, para se dedicar ao enigma de Poincaré.
Grigori Yakovlevich Perelman nasceu em Leninegrado, na União Soviética (agora São Petersburgo, Rússia), a 13 de junho de 1966 e o seu talento para a Matemática evidenciou-se cedo. Aos 10 anos, a mãe decidiu matricula-o no programa de formação Matemática de Sergei Rukshin. A sua educação continuou na Escola Secundária de Leningrado, especializada em programas avançados de Matemática e Física. Grigori destacou-se em todas as disciplinas, excepto a educação física.
Em 1982, como membro da equipa soviética na Olimpíada Internacional de Matemática, ganhou uma medalha de ouro, conseguindo pontuação máxima. No final dos anos 1980, recebeu o título “Candidate of Sciences” na Escola de Matemática e Mecânica da Universidade de Leningrado, uma das principais academias da antiga União Soviética.
5 
As formas tridimensionais têm comprimento (ou profundidade), largura e altura e estão por todo o lado, dentro de casa ou ao ar livre, podemos encontrar objetos a três dimensões onde quer que olhemos (almofadas, armários, automóveis, frutas, entre outros). Há outras classificações, como as formas unidimensionais, ou seja, possuem uma única dimensão, como será o caso, por exemplo, de uma estrada. E também as formas bidimensionais, com comprimento e largura (um campo de futebol, por exemplo).
